lunes, 25 de mayo de 2020

PERIODO2 TEMA1 GRADO6 MATE

LA MULTIPLICACIÓN DE NÚMEROS ENTEROS

RECUERDE

Tomar fotos a la actividad realizada en el cuaderno y subirla a la plataforma Classroom, colpegasus referiblemente también puede enviar a WhatsApp o correo electrónico Cada hoja debe tener su nombre completo.
Tutorías los días miércoles de 10:00am a 12:00mm

¿Cómo se multiplican los números enteros?

La multiplicación de números y el producto de números son la misma cosa, es decir, podemos utilizar el término multiplicación y el término producto y estaremos hablando de lo mismo.

Cuando tenemos una multiplicación, los números que se están multiplicando se llaman factores, por ejemplo, en la multiplicación (+2) x (+3) = (+6), los números +2 y +3 se llaman factores, y al resultado (+6) se le llama producto .

Tenemos que tener en cuenta también que el signo habitual para expresar una multiplicación o producto es el signo ‘x’ (signo por), pero a veces se expresa como simplemente un punto (·), y algunas veces no se pone ningún signo cuando multiplicamos (aunque de momento esto no lo vamos a hacer así, pero lo veremos más adelante). Por lo tanto, en esta clase, cuando haya una multiplicación de números, vamos a ver el signo (·) que nos indicará que estamos multiplicando.

Para hacer la multiplicación de números enteros (o el producto) tenemos que fijarnos siempre en los signos que llevan los factores, tenemos que ver si los factores tienen el mismo signo o si tienen diferente signo, porque esto va a determinar el signo del resultado.

Producto de dos números enteros del mismo signo

Para multiplicar dos números enteros del mismo signo, se multiplican los valores absolutos de los números (es decir, se multiplican los números sin tener en cuenta los signos que llevan) y al resultado se le pone el signo +.

(+5) · (+6) = +30 → Los factores tienen el mismo signo => El resultado es positivo.

(-4) · (-7) = +28 → Los factores tienen el mismo signo => El resultado es positivo.

Producto de dos números enteros de diferente signo

Para multiplicar dos números enteros de diferente signo, se multiplican los valores absolutos de los números (es decir, se multiplican los números sin tener en cuenta los signos que llevan) y al resultado le ponemos el signo -.

(-2) · (+3) = -6 → Los factores tienen diferentes signos => El resultado es negativo.(+6) · (-8) = -48 → Los factores tienen diferentes signos => El resultado es negativo.

La regla de los signos

Para multiplicar dos números enteros se multiplican sus valores absolutos. Si los factores tienen signos iguales, el producto es positivo, y si tienen signos distintos, el producto es negativo.

PROPIEDADES DE LA MULTIPLICACIÓN DE NÚMEROS ENTEROS

Al igual que ocurría con las propiedades de la suma, cuando hablamos de las propiedades de la multiplicación o del producto de números, estamos hablando de propiedades que ese conjunto siempre va a cumplir, es decir, un determinado conjunto de acciones que podemos aplicar siempre que queramos o necesitemos.

Las propiedades del producto de los números enteros son las siguientes:

-Propiedad conmutativa

-Propiedad asociativa

-Elemento neutro

-Propiedad distributiva

-Sacar factor común

Propiedad conmutativa del producto

La primera de las propiedades de la multiplicación de los números enteros es la propiedad conmutativa y ésta dice que al cambiar el orden de los factores, el producto no varía. Esto quiere decir que podemos multiplicar los números en el orden que queramos sin que el resultado se vea afectado.

Por ejemplo si tenemos que multiplicar +3 por -2 podemos hacerlo en ese orden o también hacer -2 por +3, y el resultado va a ser el mismo en cualquiera de los dos casos.

02-propiedad-conmutativa-del-producto-ejemplo-optimizada

Propiedad asociativa del producto

La segunda de las propiedades de la multiplicación de números enteros es la propiedad asociativa, la cual dice que la multiplicación de varios números enteros no depende de la forma en que se asocien, es decir, cuando haya solamente multiplicaciones podemos empezar a multiplicar los factores que queramos y el resultado multiplicarlo por el resto de factores (empezar a multiplicar por donde nosotros queramos, eso sí, siempre que solamente haya multiplicaciones. Cuando haya sumas o restas por el medio esto ya no lo podríamos hacer)

Ejemplo: [(+3) · (-2)] · (-5) = (+3) · [(-2) · (-5)]

04-propiedad-asociativa-del-producto-ejemplo-optimizada

La propiedad asociativa nos permite resolver productos de tres o más factores : se multiplican sus valores absolutos y al resultado se le pone el signo + si el número de factores negativos es par, o el signo – si el número de factores negativos es impar.

(+4) · (-3) · (-2) · (+5) = +120

Elemento neutro para el producto

El elemento neutro para el producto es el (+1). Esto significa que si multiplicamos cualquier número entero por (+1), el resultado va a ser el mismo número entero.

Ejemplos:

(-5) · (+1) = -5

(+1) · (-5) = -5

Propiedad distributiva del producto

La propiedad distributiva permite transformar productos en suma o restas.

Ejemplos:

(+3) · [ (-2) + (+1)] = (+3) · (-2) + (+3) · (+1)

(+3) · [ (-2) – (+1)] = (+3) · (-2) – (+3) · (+1)

Sacar factor común

Cuando en una suma o resta de productos figura un mismo factor, se puede aplicar la propiedad distributiva que, en este caso, se llama sacar factor común.

Sacar factor común es la operación contraria a la distributiva (al aplicar esta propiedad hacemos lo contrario que en la distributiva: transformamos una suma o resta en un producto.

Ejemplos:

(+3) · (-2) + (+3) · (+1) = (+3) · [ (-2) + (+1)]

(+3) · (-2) – (+3) · (+1) = (+3) · [ (-2) – (+1)]

CRITERIOS DE DIVISIVILIDAD CLIC AQUI

DIVISIÓN DE NÚMEROS ENTEROS

¿Cómo se dividen los números enteros?

En esta clase vamos a ver cómo se hace la división de números enteros. Solamente vamos a ver las divisiones exactas, que son las que dan como resultado (cociente) otro número entero. Más adelante en otras clases explicaremos las divisiones inexactas.
Para hacer la división de números enteros, se divide el valor absoluto del dividendo entre el valor absoluto del divisor, y al cociente se le añade el signo según la regla de los signos para la división. Es decir, hacemos la división sin tener en cuenta los signos, como una división de números naturales, y luego le ponemos al cociente el signo que le corresponda.
La regla de los signos para la división de números enteros dice que si los signos del dividendo y del divisor son iguales el signo del cociente será positivo y si los signos del dividendo y del divisor son distintos, el signo del cociente será negativo:

Regla de los signos para la división.
Ejemplos:
(+40) : (+5) = +8
(-20) : (-2) = +10
(+100) : (-25) = -4
(-80) : (+2) = -40

Qué son los números primos?

Los números primos son aquellos que solo son divisibles entre ellos mismos y el 1, es decir, que si intentamos dividirlos por cualquier otro número, el resultado no es entero. Dicho de otra forma, si haces la división por cualquier número que no sea 1 o él mismo, se obtiene un resto distinto de cero.

Tabla de números primos hasta el 100

Vamos a construir la tabla de todos los números primos que existen hasta el 100.
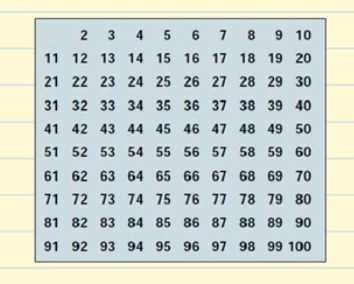
Vamos a empezar con el 2. El 2 es un número primo pero todos lo múltiplos de 2 serán números compuestos, ya que serán divisibles entre 2. Tachamos de nuestra tabla todos los múltiplos de 2.
El siguiente número primo es el 3, por lo tanto podemos tachar todos los múltiplos de 3, ya que serán números compuestos.
El siguiente número primo es el 5, por lo que tachamos todos los múltiplos de 5.
El siguiente número primo es el 7, así que tachamos todos los múltiplos de 7.
El siguiente número primo es el 11, por lo que tachamos todos los múltiplos de 11, que son el 22, 33, 44, 55, 66, 77, 88, y el 99. Todos estos ya habían sido tachados con anterioridad, por lo que ya hemos terminado de tachar todos los números compuestos de nuestra tabla.
Esta es nuestra lista de números primos del 1 al 100. No es necesario que te los aprendas de memoria, pero si que te acuerdes de los más pequeños, como el 2, 3, 5, 7, 11, 13.

TEMA4 GRADO6 PERIODO1 MATE

PROYECTO TANGRAM

Descargar guía

RECUERDE

Tomar fotos a la actividad realizada en el cuaderno y subirla a la plataforma Classroom, colpegasus referiblemente también puede enviar a WhatsApp o correo electrónico Cada hoja debe tener su nombre completo.
Tutorías los días miércoles de 10:00am a 12:00mm

El tangram es un juego chino muy antiguo, especie de rompecabezas, que está compuesto por 7 piezas: un paralelogramo (romboide), un cuadrado y 5 triángulos. El objetivo de este juego es crear figuras utilizando las 7 piezas. Las piezas deben tocarse pero no superponerse.

Normalmente los "Tans" se guardan formando un cuadrado. Existen varias versiones sobre el origen del tangram, una de las más famosas con el vocablo latino "grama" que significa escrito o gráfico. Otra versión dice que el origen del juego se remonta a los años 618 a 907 de nuestra era, época en la que reinó en China la dinastía Tang de donde se derivaría su nombre.

Cómo hacer un Tangram paso a paso en casa

Para fabricar tu propio Tangram sigue estas sencillas indicaciones.

Lo que necesitas para fabricar un Tangram propio

Listado de elementos y herramientas que vamos a necesitar para empezar a construir nuestro juego tangram:

El material base donde dibujaremos el esquema del tangram y recortaremos las piezas que lo forman. Este puede ser fomi, icopor reciclado o cartón reciclado.
Herramienta de corte como cutter, bisturí o tijera.
Un lápiz
Una regla
Marcador para colorear o pintura para personalizar las piezas. Esto es opcional
Papel bond o cartulina para elaborar la plantilla.

Pasos a dar para hacer tu propio Tangram

Paso 1: dibujar con lápiz en el material elegido para la plantilla un cuadrado, además de cuatro divisiones iguales en formas de columnas y otras cuatro en forma de filas, tal y como se muestra en la imagen. Los 16 cuadrados resultantes nos servirá como guías para realizar las siguientes líneas.

Paso 2: pegar la platilla en el fomi, icopor o cartón (también puede dibujar la plantilla directamente en estos materiales) aprovechando las guías de la plantilla dibujadas en el paso anterior, ahora dibujamos con el lápiz o marcador fino y de manera más intensa las nuevas líneas tal y como se muestran en la siguiente ilustración.

Paso 3: ahora recortar las piezas que hemos dibujado ayudándonos del cutter, bisturí o tijera. Nos tienen que salir 7 piezas denominadas “Tans”, dos triángulos grandes, uno mediano, dos pequeños, un cuadrado y un romboide.

Paso 4: En este paso ya lo único que queda es personalizar los Tans pintándolos del color que nosotros queramos con la ayuda de un pincel y acuarela o con marcadores.

Paso final: Ya tienes tu juego terminado, adicionalmente puedes construir una caja cuadrada para guardar tu juego. Así que ahora ya sólo queda encontrar figuras Tangram y empezar a jugar.

Figuras tangram

¡¡Vamos a Jugar!

Arma con los 7 polígonos el juego tangram las siguientes figuras

PERIODO2 TEMA1 GRADO10

martes, 19 de mayo de 2020

TEMA3 PERIODO1 GRADO6 MATE

ÁNGULOS, MEDICIÓN Y CONSTRUCCIÓN

Descargar guía

RECUERDE

Tomar fotos a la actividad realizada en el cuaderno y subirla a la plataforma Classroom, colpegasus referiblemente también puede enviar a WhatsApp o correo electrónico Cada hoja debe tener su nombre completo.
Tutorías los días miércoles de 10:00am a 12:00mm

Un ángulo es la región del plano comprendida entre dos semirrectas con origen común.A las semirrectas se las llama lados y al origen común vértice.

Angulo agudo representación gráfica

Medición de ángulos

Para medir ángulos utilizamos el grado sexagesimal $(^{\circ })$

Grado sexagesimal es la amplitud del ángulo resultante de dividir la circunferencia en $360$ partes iguales.

$1^{\circ }=60'=3600''$

$1'=60''$

Radián

Radián (rad) es la medida del ángulo central de una circunferencia cuya longitud de arco coincide con la longitud de su radio.

$1\: \textup{rad}=57^{\circ}\, 17'\, 44.8''$

$360^{\circ}=2\pi \textup{rad}$

Clasificación de ángulos según su medida

Ángulo agudo

Definición de un ángulo agudo representación gráfica Mide menos de $90^{\circ}$ .

Ángulo recto

Ángulo recto representación gráfica Mide $90^{\circ}$ .

Ángulo obtuso

Ángulo obtuso representación gráfica Mide más de $90^{\circ}$ .

Ángulo llano

Ángulo llano representación gráfica Mide $180^{\circ}$ .

Ángulo convexo

Ángulo convexo representación gráfica Mide menos que un ángulo llano.

Ángulo cóncavo

Ángulo cóncavo representación gráfica Mide más que un ángulo llano.

Ángulo nulo

Ángulo nulo representación gráfica Mide $0^{\circ}$ . Las semirrectas que forman los ángulos coinciden.

Ángulo completo

Ángulo completo representación gráfica Mide $360^{\circ}$ .

Ángulo negativo

Ángulo negativo representación gráfica Mide menos de $0^{\circ}$ .

Los ángulos negativos giran en el sentido horario, es decir, en el sentido en que se mueven las agujas de un reloj.

Un ángulo negativo lo podemos transformar en un ángulo positivo sumándole $360^{\circ}$ .

$-30^{\circ}=360^{\circ}-30^{\circ}=330^{\circ}$

Ángulo mayor de 360°

Ángulo mayor a 360 grados representación gráfica Mide más de una vuelta.

Un ángulo de $390^{\circ}=360^{\circ}+30^{\circ}$ , si lo representamos coincide con un ángulo de $30^{\circ}$ . Un ángulo de $750^{\circ}=2\cdot 360^{\circ}+30^{\circ}$ , si lo representamos coincide con un ángulo de $30^{\circ}$ . Si queremos pasar un ángulo a la primera vuelta, dividimos el ángulo entre $360^{\circ}$ : El cociente es el número de vueltas que da.El resto es ángulo resultante que corresponde a la primera vuelta.

Clasificación de ángulos según su posición

Ángulos consecutivos

Son aquellos que tienen el vértice y un lado común.

Ángulos adyacentes

Son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en polongación del otro.

Forman un ángulo llano.

Ángulos opuestos por el vértice

Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.

Los ángulos $1$ y $3$ son iguales.

Los ángulos $2$ y $4$ son iguales.

Clasificación de ángulos según su suma

Ángulos complementarios

Dos ángulos son complementarios si suman $90^{\circ}$ .

Ángulos suplementarios

Dos ángulos son suplementarios si suman $180^{\circ}$ .

Ángulos entre paralelas y una recta transversal

Ángulos correspondientes

Los ángulos $1$ y $2$ son iguales.

Ángulos alternos internos

Los ángulos $2$ y $3$ son iguales.

Ángulos alternos externos

Los ángulos $1$ y $4$ son iguales.

Ángulos en la circunferencia

Ángulo central

El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.

La medida de un arco es la de su ángulo central correspondiente.

${\widehat{AOB}}=\stackrel{\textstyle\frown}{AB}$

Ángulo inscrito

El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.

Mide la mitad del arco que abarca.

${\widehat{AOB}}=\cfrac{1}{2}\stackrel{\textstyle\frown}{AB}$

Ángulo semi-inscrito

El vértice de ángulo semi-inscrito está en la circunferencia, un lado secante y el otro tangente a ella.

Mide la mitad del arco que abarca.

Ángulo semi inscrito representación gráfica

${\widehat{AOB}}=\cfrac{1}{2}\stackrel{\textstyle\frown}{AB}$

Ángulo interior

Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

${\widehat{AOB}}=\cfrac{1}{2}(\stackrel{\textstyle\frown}{AB}+\stackrel{\textstyle\frown}{CD})$

Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella.